Summary:

Graph Neural Networks have become popular recently and involve learning from graph data. They have many applications in recommendation systems, predicting uses and structures of molecules, etc. Many of the graphs involved are very large, like the social media network of Facebook and the product-customer network of Amazon, having millions or billions of nodes. it is impossible to train GNNs on them on a single CPU. Thus the authors have proposed DistDGL, a distributed GNN development framework. It builds on the existing DGL framework and extends it to allow the training of GNNs using multiple CPUs. This problem of training on large graphs has been under research for some time, and there have been existing works in this area and frameworks like Euler. However, most of these frameworks focus on full graph training using a distributed setting. The authors believe this method is inefficient and leverage the mini-batch training approach, which has been widely adopted. Some frameworks that use mini-batch training do not have locality-aware partitioning, which the authors have used in their work and achieved good performance. The authors have proposed many things like graph partitioning, distributed key-value storage, sampling, and mini-batch training. The frameworks seem to achieve good speed-ups against existing frameworks like Euler and PyTorch.

Main Contribution:

The main contributions are quoted from the paper:

1. An adapted version of METIS for locality-aware partitioning that not only minimises the edges across partitions but also balances the load on each trainer such that the whole network can be trained efficiently
2. A distributed Key-Value store that allows for efficient access to graph structures like nodes, edges and embeddings, thus reducing communication overhead in the distributed setting.
3. A distributed sampler that samples efficiently reduces communication costs by hiding it under the training computation. The result is the DistDGL framework that extends the existing DGL framework and achieves 2.2× speedup over Euler on a cluster of four CPU machines. It can scale up for the GraphSage model on a graph with 100 million nodes and 3 billion edges and trains it in 13s per epoch on 16 CPUs

Specific Comments:

• The novelty lies in the different optimisations they make in the distributed architecture to speed up the training.
• The authors run their experiments only for the node classification task for the framework evaluation and believe that the results will be similar for the other tasks as well. This seems reasonable as the model architecture is mostly the same, and the only change is in the objective function.
• For most of the features added, only the high-level description has been given. More depth should have been provided, especially for the partitioning algorithm.
• The paper is interesting because it combines many different ideas to develop a single framework for efficiently training GNNs in a distributed manner.

Detailed Analysis of the solution approach:

DistDGL does the following:

1. Preprocess the graph by partitioning it in a locality-aware manner so that most nodes and features are available locally to the trainer while training.
2. Storage of graph structure and features using a distributed Key-Value store that uses different optimisation techniques to quickly make the data required by trainers available.
3. Distributed sampling that samples efficiently overlaps the communication cost with the training computation.
4. Finally, mini-batch training on the samples on each machine and then aggregating the gradients and using them to update each of the local models on the trainers.

   Locality-Aware Partitioning using METIS:

   • Metis tries to partition the graph to minimise the edges across the positions and only balances the number of vertices in the graph. This is insufficient for mini-batch training, which requires the same number of batches from each partition per epoch and all batches to have roughly the same size.
   • They formulate this load-balancing problem as a multi-constraint partitioning problem, which balances the partitions based on user-defined constraints.
   • They extended METIS to only retain a subset of the edges in each successive graph so that the degree of each coarse vertex is the average degree of its constituent vertices. This ensures that as the number of vertices in the graph reduces by approximately a factor of two, so do the edges.
   • In addition, to further reduce the memory requirements, they use an out-of-core strategy for the coarser/finer graphs that are not being processed currently
   • The set of optimizations above compute high-quality partitionings requiring 5× less memory and 8× less time than METIS’ default algorithms.
   • To save memory for maintaining the mapping between global IDs and local IDs, DistDGL relabels vertex IDs and edge IDs of the input graph during graph partitioning to ensure that all IDs of core vertices and edges in a partition fall into a contiguous ID range. In this way, mapping a global ID to a partition is binary lookup in a very small array and mapping a global ID to a local ID is a simple subtraction operation.

     Distributed Key-Value Store:

   • instead of using an existing distributed in-memory KVStore, such as Reddis, for (i) better co-location of node/edge features in KVStore and graph partitions, (ii) faster network access for high-speed network, (iii) efficient updates on sparse embeddings.
   • Instead of going through Inter-Process Communication (IPC), the KVStore server shares all data with the trainer process via shared memory. Thus, trainers can access most of the data directly without paying any overhead of communication and process/thread scheduling.
   • An optimized RPC framework for fast networking communication, which adopts zero-copy mechanism for data serialization and multithread send/receive interface.
   • In addition to storing the feature data, we design DistDGL’s KVStore to support sparse embedding for training transductive models with learnable vertex embeddings.

     Distributed Sampler:

   • issuing sampling requests to the sampling workers, trainers overlap the sampling cost with minibatch training. When a sampling request goes to the local sampler server, the sampling workers to access the graph structure stored on the local sampler server directly via shared memory to avoid the cost of the RPC stack. The sampling workers also overlaps the remote RPCs with local sampling computation by first issuing remote requests asynchronously. This effectively hides the network latency because the local sampling usually accounts for most of the sampling time.

     Mini-batch trainer:

   • Mini-batch trainers run on each machine to jointly estimate gradients and update parameters of users’ models.
   • Each trainer samples data points uniformly at random to generate mini-batches independently.
   • To balance the computation in each trainer, DistDGL uses a two-level strategy to split the training set evenly across all trainers at the beginning of distributed training.
   • Essentially, we make a tradeoff between load balancing and data locality
   • In terms of parameter synchronization, we use synchronous SGD to update dense model parameters.
   • Concurrent updates from multiple trainers rarely result in conflicts because mini-batches from different trainers run on different embeddings.

Detailed Analysis of the experiments:

Focus only on the node classification task. Benchmarking done on GraphSAGE model using OBGN products and papers graphs given below:

They use a cluster of eight AWS EC2 m5n.24xlarge instances (96 VCPU, 384GB RAM each) connected by a 100Gbps network. In all experiments, they use DGL v0.5 and Pytorch 1.5. For Euler experiments, they use Euler v2.0 and TensorFlow 1.12.

Comparison with Euler:

Euler is designed for mini-batch training in a distributed setting. It parallelises computation with multiprocessing and uses one thread for forward and backward computation and sampling inside a trainer, which is quite different from DistDGL. For a fair comparison, they use the same global batch size in both networks and run synchronous SGD. DistDGL gets 2.2× speedup over Euler in all different batch sizes. For a particular batch size, they also compare the time required in each individual step and find that the main speed is 5x in the data-copy step. This is because of the locality-aware partitioning and sampling of DistDGL, which reduces the communication cost while training.

DistDGL’s sparse embedding vs Pytorch’s sparse embedding:

The GraphSage model with DistDGL’s sparse embeddings on OGBN-PRODUCT graph gets almost 70× speedup over the version with Pytorch sparse embeddings. This is because of the KV store and co-location of data, while in PyTorch there is a communication overhead of allreduce.

Scalability:

The DistDGL scales quite well, requiring only 13 seconds to train per epoch the GraphSage model on the OGBN-PAPERS100M graph in a cluster of 16 m5.24xlarge machines. DistDGL running on a single machine with two trainers, outperforms DGL. This may attribute to the different multiprocessing sampling used by the two frameworks. DGL relies on Pytorch data loaders multiprocessing to sample mini-batches, while DistDGL uses dedicated sampler processes to generate mini-batches. Not only is speed increased, but accuracy is maintained as well.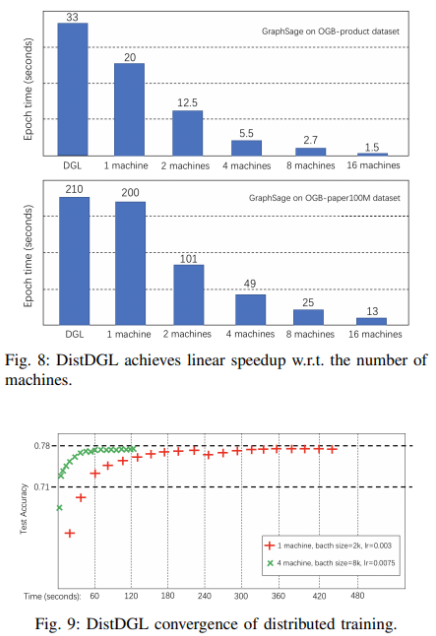

Comments on possible extensions and Conlusion:

The paper is complete in the sense that it gives an end-to-end distributed framework for training GNNs. It speeds up the process significantly and is also able to handle very large graphs with millions or billions of nodes. Possible extensions include trying more partitioning approaches that make it more efficient, trying to achieve better accuracy than training on a single machine, and using model aggregation which involves aggregating all the local models trained on each of the trainers.

Paper Link